
Each of the following blocks first designs a filter using the simplified (recommended) API, and then designs the same filter using the Scipy-compatible API. filter_type_hilbert : filter with odd symmetry, that is, type III (for even order) or type IV (for odd order) linear phase filters.Ĭompare the examples with the simplified API and the Scipy API.Odd symetric as in filter_type_hilbert case, but with a linear sloping desired response. filter_type_differentiator : frequency proportional response in bands.filter_type_bandpass : flat response in bands.filter_type::RemezFilterType: Default is filter_type_bandpass.The length of weight has to be half the length of bands. weight::Vector: (optional) A relative weighting to give to each band region.desired::Vector:A sequence half the size of bands containing the desired gain in each of the specified bands.All elements must be non-negative and less than half the sampling frequency as given by Hz. bands::Vector: A monotonic sequence containing the band edges in Hz.Below the arguments and examples are described that differ from the simplified API version.
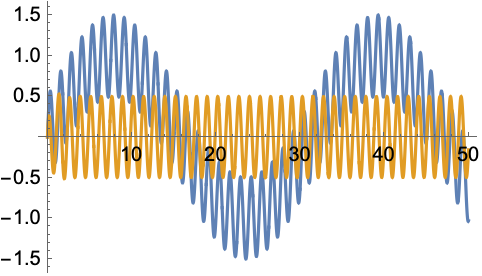
The filters designed are equivalent, the inputs are just specified in a different way. For a simplified API, see the 2 argument version (numtaps, band_defs). This is the scipy compatible version that requires 3 arguments (numtaps, bands, desired). Inverse sinc filter - custom response function julia> L = 64 Fs = 4800*L julia> h = remez(180, Hz=2.0, maxiter=30) Įxamples from the unittests - Odd-symmetric filters - hilbert and differentiators type.Įven length - has a much better approximation since the response is not constrained to 0 at the nyquist frequency. Julia> plot(f, 20*log10.(abs.(freqresp(b2,f,1.0))))Įxamples from the unittests - standard (even) symmetry. Here we compute the frequency responses and plot them in dB. Here is a bandpass filter with the same passband, but wider transition bands. The wider the transition bands, the lower the maximum error in the bands specified. You can trade-off maximum error achieved for transition bandwidth. Note: the behavior in the frequency ranges between those bands - the transition bands - is unspecified. 506-525, 1973.Ĭonstruct a length 35 filter with a passband at 0.15-0.4 Hz (desired response of 1), and stop bands at 0-0.1 Hz and 0.45-0.5 Hz (desired response of 0).

Rabiner, A Computer Program for Designing Optimum FIR Linear Phase Digital Filters, IEEE Trans. Parks, A unified approach to the design of optimum FIR linear phase digital filters, IEEE Trans. PolynomialRatio: A rank-1 array containing the coefficients of the optimal (in a minimax sense) filter.

For example: julia> H = PolynomialRatio(, )
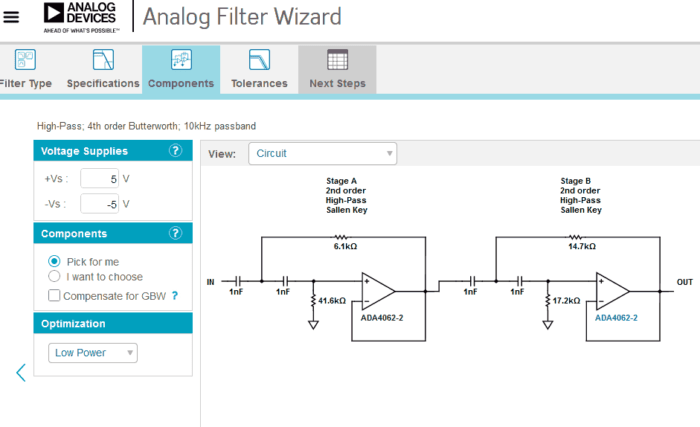
#ANALOG FILTER DESIGNER SERIES#
These filter coefficient objects support the following arithmetic operations: inversion ( inv), multiplication ( *) for series connection, and integral power ( ^) for repeated mutlpilcation with itself. biquads must be specified as a vector of Biquads. Filter representation in terms of a cascade of second-order sections and gain.


 0 kommentar(er)
0 kommentar(er)
